堆的定义
堆在逻辑上是一种完全二叉树,物理结构上是一维数组,按照根节点大小分为最大堆和最小堆,如下图。
最小堆:所有节点的左右孩子节点都大于或者等于父节点
最大堆:所有节点的左右孩子节点都小于或者等于父节点
补充:完全二叉树的性质
如果有一颗有n个节点的完全二叉树的节点按层次序编号,对任一层的节点i(0<=i<=n)有(注意i的取值)
1.如果i=0,则节点是二叉树的根,无双亲,如果i>0,则其双亲节点为[i/2],向下取整
2.如果2i+1>n那么节点i没有左孩子,否则其左孩子为2i+1
3.如果2i+2>n那么节点没有右孩子,否则右孩子为2i+2
堆的特性
- 堆是弱序的,所以遍历堆是很难的,基本堆都不支持遍历。
- 堆一般都是用来实现优先级队列,由它实现的优先级队列的插入和删除的时间复杂度都是O(logn)。
堆的操作
插入
把插入的节点放在数组尾部,然后向上筛选。
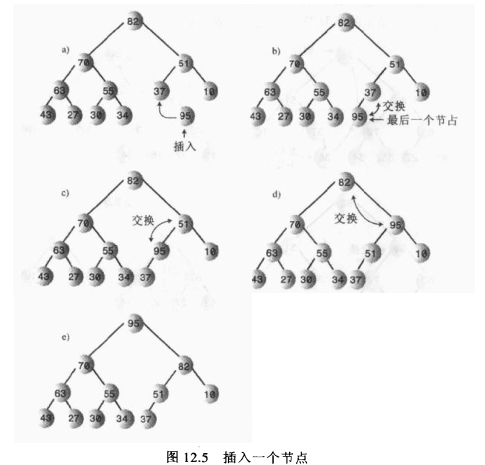
移除
把根节点移除,然后向下筛选。
移走根
把最后一个节点移动到根的位置
一直向下筛选这个节点,直到它在一个大于它的节点之下,小于它的节点之上为止。
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
| package com.czj.example01;
import java.lang.reflect.Array;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Random;
/**
* 创建在 2020/4/30 23:17
*/
public class Heap<T extends Comparable<? super T>>{
private final Object[] items;
private Comparator comparable;
private int currentIndex = 0;
private static final int DEFAULT_CAPACITY = 10;
public Heap(){
this(DEFAULT_CAPACITY);
}
public Heap(int capacity){
this(capacity,null);
}
public Heap(int capacity,Comparator comparable){
this.items = new Object[capacity];
this.comparable = comparable;
}
/**
* 添加元素,成功返回true,否则返回false
* @author czj
* @date 2020/4/30 23:29
* @param [item]
* @return boolean
*/
public boolean add(T item){
//堆已满返回false
if (isFull()){
return false;
}
items[currentIndex] = item;
adjustUp();
currentIndex++;
return true;
}
public boolean isFull(){
return items.length == currentIndex;
}
public boolean isEmpty(){
return items.length==0;
}
/**
* @author czj
* 将新增的元素向上调整到合适的位置
* @date 2020/4/30 23:33
* @param []
* @return void
*/
public void adjustUp(){
T temp=null;
T item=null;
T parentItem=null;
int parentIdx = (currentIndex-1)/2;
int nowIdx=currentIndex;
int num = -1;
while (nowIdx>0){
item = (T) items[nowIdx];
parentItem = (T) items[parentIdx];
if (comparable==null){
num = item.compareTo(parentItem);
}else {
num = comparable.compare(item,parentItem);
}
if (num<0){
break;
}
items[nowIdx]=parentItem;
items[parentIdx]=item;
nowIdx=parentIdx;
parentIdx=(nowIdx-1)/2;
}
}
/**
* @author czj
* 向下调整
* @date 2020/5/2 15:31
* @param []
* @return void
*/
public void adjustDown(){
T item = (T) items[0];
int bigIdx=0,index=0;
int leftIdx=0,rightIdx=0;
T leftItem=null,rightItem=null;
int num=0;
while (index<currentIndex/2){
leftIdx = 2*index+1;
rightIdx = leftIdx+1;
if (rightIdx<currentIndex) {
leftItem = (T) items[leftIdx];
rightItem = (T) items[rightIdx];
if (comparable == null) {
bigIdx = leftItem.compareTo(rightItem)>=0?leftIdx:rightIdx;
} else {
bigIdx = comparable.compare(leftItem, rightItem)>=0?leftIdx:rightIdx;
}
}else {
bigIdx = leftIdx;
}
items[index]=items[bigIdx];
index=bigIdx;
}
items[index]=item;
}
public T remove(){
if (isEmpty()){
return null;
}
T item = (T) items[0];
items[0]=items[--currentIndex];
adjustDown();
return item;
}
public int size(){
return items.length;
}
}
|




